In this tutorial I’m going to introduce you to the techniques used to draw 3D stuff with Core Animation.
The good news are Core Animation can help us achieve some 3D goodness without using OpenGL directly. There are bad news though: creating a complex 3D video game with Core Animation is not a good idea.
In the first part of this tutorial we’ll discuss some 3D theory and we’ll create some simple 3D scenes using the concepts described.
In the second part we’ll use Core Animation to create a 3D scene that should remind you the interface used in a carousel image gallery.
Here’s a preview of the final app in action.
Ready? Let’s get the coding started!
First, download the code at the end of the article. If you want to create your own project remember to add the QuartzCore framework to it.
3D and Matrices (a bit of math… but just a bit!)
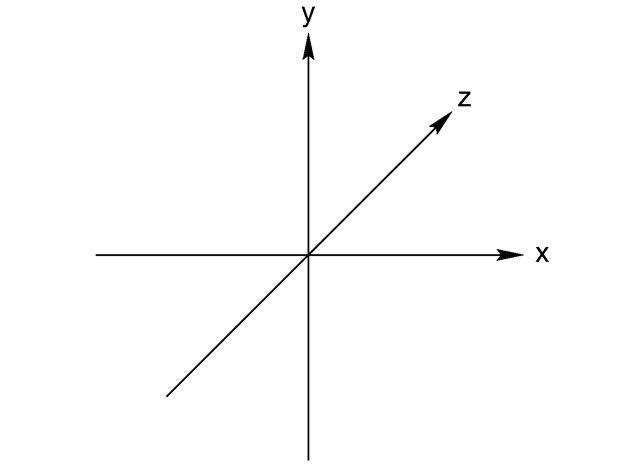
Drawing into a 3D space means adding depth to the standard X and Y 2D space we are used to in iOS. This results in a third axis called Z.
In that space we can move an object vertically, horizontally and by depth simply by changing its X,Y,Z coordinates.
Performing transformations like translation, scale and rotation to an object in a 2D or 3D space needs some math calculations.
Using matrices is the right way to implement these operations.
You can think of a matrix as a grid of values in some ways similar to a multi dimensional array.
For example, in 3D spaces we use a 4X4 Matrix like this:
[X][0][0][0]
[0][Y][0][0]
[0][0][Z][0]
[0][0][0][1]
Multiplying this matrix by the coordinate of each point of an object (in 3D they are also called vertices), we obtain a transformation of the original object.
To be precise the previous matrix is used to perform the scale operation, where X, Y and Z represent the scale values that you want to apply for each axis.
If you need to perform other transformations, like rotation or translation, you’ll have to set the matrix with a different scheme.
Fear not, you don’t need to know more than that and you are not supposed to do this operation directly. Core Animation does it for you in a totally opaque way.
Personally, I feel more confident with my code if I know how it works in the background (the basics of it, at least). So if you want to know more about matrices I suggest you to take a look at this article.
3D Transformations
Now that you have a basic idea of what a matrix does and how a 3D space is organised let’s do some 3D stuff using Core Animation.
Open the file TB_3DIntro->viewController.m.
I have listed 6 functions prefixed with A,B,C,D,E, or F. Each function creates a different 3D scene.
Let’s see the scene created by the function A_singlePlan.
With this function we are going to draw a plan rotated by 45 degrees on the Y axis.
First, we create a CALayer that we use as container (it is not required, but I prefer not to work directly with the first view’s layer).
- (void)A_singlePlane{
//Create the container
CALayer *container = [CALayer layer];
container.frame = CGRectMake(0, 0, 640, 300);
[self.view.layer addSublayer:container];
Then we create another CALayer to represent a plane.
//Create a Plane
CALayer *purplePlane =
[self addPlaneToLayer:container
size:CGSizeMake(100, 100)
position:CGPointMake(100, 100)
color:[UIColor purpleColor]];
I’ve built a simple helper function which adds the plane to the container layer directly and then returns the new plane layer. Its code is extremely simple:
-(CALayer*)addPlaneToLayer:(CALayer*)container size:(CGSize)size position:(CGPoint)point color:(UIColor*)color{
//Initialize the layer
CALayer *plane = [CALayer layer];
//Define position,size and colors
plane.backgroundColor = [color CGColor];
plane.opacity = 0.6;
plane.frame = CGRectMake(point.x, point.y, size.width, size.height);
plane.borderColor = [[UIColor colorWithWhite:1.0 alpha:0.5]CGColor];
plane.borderWidth = 3;
plane.cornerRadius = 10;
//Add the layer to the container layer
[container addSublayer:plane];
return plane;
}
And finally we add the transformation using a CATransform3D.
What’s a CATransform3D??? Cmd+click on the data type name and you get that it’s a structure which represent a matrix using an “exotic” syntax 😛
struct CATransform3D
{
CGFloat m11, m12, m13, m14;
CGFloat m21, m22, m23, m24;
CGFloat m31, m32, m33, m34;
CGFloat m41, m42, m43, m44;
};
typedef struct CATransform3D CATransform3D;
The code of the transformation part is extremely simple:
//Apply the transform to the PLANE
CATransform3D t = CATransform3DIdentity;
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 1, 0);
purplePlane.transform = t;
}
The first step is to initialize the transformation using the identityMatrix (CATransform3DIdentity), that is nothing more than a neutral value (like 0 for the sum) and we multiply that by a rotation matrix using the function CATransform3DRotate.
This function takes a starting matrix, the angle of the rotation (in radians) and the influence over the 3 axis. In the example X and Z are not influenced by the rotation while the Y is totally influenced… that just means that the object rotates by 45° around the Y axis.
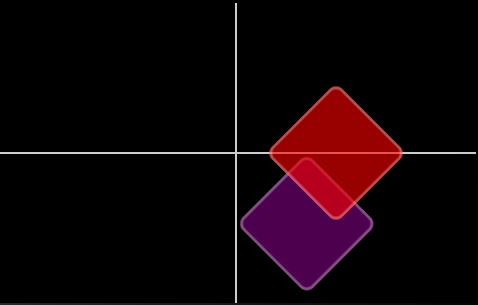
This is the scene produced by this first example.
Uhm… as you can see it doesn’t look 3D at all! We have just a square squeezed on the X axis.
The problem is that we haven’t specified a perspective value. Normally a 3D scene is drawn using a Orthographic projection that creates a flattened representation of the scene. In other words in an orthographic projection you can’t notice the depth produced by the Z axis.
To add depth to our scene we have to modify the param m34 of the transform matrix. This parameter defines the perspective value.
Let’s move to the function B_singlePlanePerspective to see how it works.
The code of this function is identical to the previous function except for the transformation part:
//Apply transformation to the PLANE
CATransform3D t = CATransform3DIdentity;
//Add the perspective!!!
t.m34 = 1.0/ -500;
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 1, 0);
purplePlane.transform = t;
As you can see we can directly access the m34 property and assign it an arbitrary value.
I won’t go deeper in math explanation about how this value is going to modify the scene, but let’s say that the closer it is to 0 the deepest is the perspective.
Here the result of this code with 2 different perspective values:
3D Transformations chain
To perform more than one transformation on an object we can perform multiplication of matrices.
For example if we want to translate and rotate an object we can obtain a transformation matrix just multiplying 2 matrices:
TransformMatrix = TranslateMtx * RotateMtx
In arithmetics we are used to apply the commutative property:
TranslateMtx * RotateMxt = RotateMtx * TranslateMtx
But Matrix multiplication is not commutative! So AxB could be different from BxA. This is a really important point to keep in mind!
In the next example (function C_transformationsChain) we are going to perform the same transformations on 2 objects just changing the order with which those transformations are applied. Here’s the main code:
//Apply transformation to the PLANES
CATransform3D t = CATransform3DIdentity;
//Purple plane: Perform a rotation and then a translation
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 0, 1);
t = CATransform3DTranslate(t, 100, 0, 0);
purplePlane.transform = t;
//reset the transform matrix
t = CATransform3DIdentity;
//Red plane: Perform translation first and then the rotation
t = CATransform3DTranslate(t, 100, 0, 0);
t = CATransform3DRotate(t, 45.0f * M_PI / 180.0f, 0, 0, 1);
redPlane.transform = t;
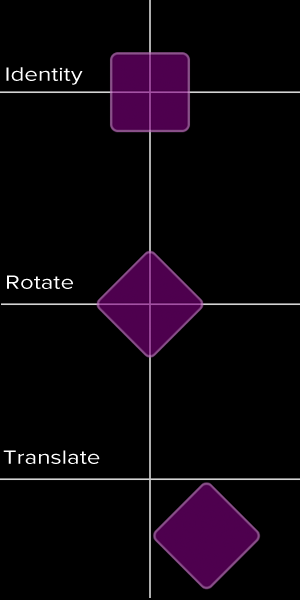
And now take a look at the result
As you can see the order of the transformation radically changes the way the 2 objects are placed in space.
Let’s focus on the PurplePlane: In this case the rotation changes its axis orientations.
Next we translate the PurplePlane on a X axis that is oriented in a different way respect to the RedPlane axis.
Check these images to better understand how the transformations take place.
Work with layer hierarchies
Have you noticed that until now we have applied transformations directly to the planes? In a 3D scene it is often useful to create hierarchies of objects and applying transformations to the root of the hierarchy, transforming then the whole structure.
Let’s take the example produced by the function D_multiplePlanes.
We add 4 planes to the container.
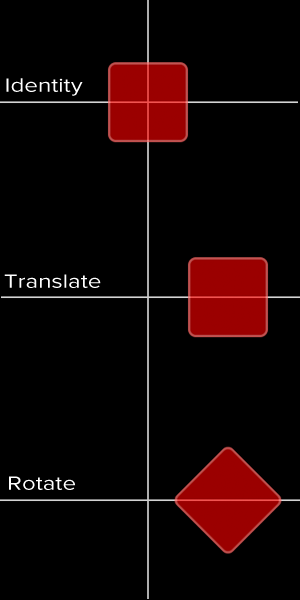
Without any transformations the scene would look like this:
Adding a rotation to the Y axis to each plane we obtain 4 distinct rotations:
But performing the rotation on the container we get a totally different scene:
We can think of this last scene as the result of a camera position change. So we are not moving each plane but we are changing our point of view.
I write here the part of the function that applies the transformations to the planes or to the container:
//Transformation
CATransform3D t = CATransform3DIdentity;
BOOL applyToContainer = NO;
//Apply the transformation to each PLANE
if(!applyToContainer){
t.m34 = 1.0 / -500.0;
t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
purplePlane.transform = t;
t = CATransform3DIdentity;
t.m34 = 1.0 / -500.0;
t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
redPlane.transform = t;
t = CATransform3DIdentity;
t.m34 = 1.0 / -500.0;
t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
orangePlane.transform = t;
t = CATransform3DIdentity;
t.m34 = 1.0 / -500.0;
t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
yellowPlane.transform = t;
}
//Apply the transformation to the CONTAINER
else{
CATransform3D t = CATransform3DIdentity;
t.m34 = 1.0/-500;
t = CATransform3DRotate(t, degToRad(60.0), 0, 1, 0);
container.transform = t;
}
Work with CATransformLayer
What we have seen so far works correctly, but to be honest the CALayer is not the right choice as the root of a 3D hierarchy.
The function E_multiplePlanesZAxis is going to show us why.
In this scene we create 4 planes at the same X, Y coordinates but with different Z.
The purplePlane turns out to be the closest to your point of view and the YellowPlane the farthest.
//Apply transforms to the PLANES
t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -10);
purplePlane.transform = t;
t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -50);
redPlane.transform = t;
t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -90);
orangePlane.transform = t;
t = CATransform3DIdentity;
t = CATransform3DTranslate(t, 0, 0, -130);
yellowPlane.transform = t;
Before creating these planes, we apply a rotation to the container as we did in the previous example.
//Apply transform to the CONTAINER
CATransform3D t = CATransform3DIdentity;
t.m34 = 1.0/-500;
t = CATransform3DRotate(t, 80.0f * M_PI / 180.0f, 0, 1, 0);
container.transform = t;
You’d probably expect to see something like this:

This is due to the fact that a CALayer is incapable of managing the depth of a 3D hierarchy and it just flattens the scene to a single Z level.
To correct this problem and obtain the right result, we have to choose a CATransformLayers as root object.
Check the function F_multiplePlanesZAxis which fixes the problem:
//Create the container as a CATransformLayer
CATransformLayer *container = [CATransformLayer layer];
container.frame = CGRectMake(0, 0, 640, 300);
[self.view.layer addSublayer:container];
Remember that the CATransformLayer is a special layer. Unlike CAlayers only its sublayers are rendered and properties like backgroundColor, contents, border etc are totally ignored.
The first part of this tutorial is finished. I suggest you to play with these functions and, why not, try to apply the scale transformation using CATransform3DScale that I haven’t shown you in this tutorial.
If you have any questions you can find me on twitter @bitwaker.
Yari D'areglia
https://www.thinkandbuild.itCEO at Nexent.io by day, indie game developer by night. I also run the blog indiegames.wtf.